Dist Plot

Authors

[Editor] Hu Zheng;

[Contributors]

Modified

2026-01-27

Note

Hiplot website

This page is the tutorial for source code version of the Hiplot Dist Plot plugin. You can also use the Hiplot website to achieve no code ploting. For more information please see the following link:

https://hiplot.cn/basic/ggdist?lang=en

The dist plot is a visual diagram using a confidence distribution.

Setup

  • System Requirements: Cross-platform (Linux/MacOS/Windows)

  • Programming language: R

  • Dependent packages: data.table; jsonlite; ggdist; tidyr; broom; modelr; ggplot2

# Install packages
if (!requireNamespace("data.table", quietly = TRUE)) {
  install.packages("data.table")
}
if (!requireNamespace("jsonlite", quietly = TRUE)) {
  install.packages("jsonlite")
}
if (!requireNamespace("ggdist", quietly = TRUE)) {
  install.packages("ggdist")
}
if (!requireNamespace("tidyr", quietly = TRUE)) {
  install.packages("tidyr")
}
if (!requireNamespace("broom", quietly = TRUE)) {
  install.packages("broom")
}
if (!requireNamespace("modelr", quietly = TRUE)) {
  install.packages("modelr")
}
if (!requireNamespace("ggplot2", quietly = TRUE)) {
  install.packages("ggplot2")
}

# Load packages
library(data.table)
library(jsonlite)
library(ggdist)
library(tidyr)
library(broom)
library(modelr)
library(ggplot2)
sessioninfo::session_info("attached")
─ Session info ───────────────────────────────────────────────────────────────
 setting  value
 version  R version 4.5.2 (2025-10-31)
 os       Ubuntu 24.04.3 LTS
 system   x86_64, linux-gnu
 ui       X11
 language (EN)
 collate  C.UTF-8
 ctype    C.UTF-8
 tz       UTC
 date     2026-01-27
 pandoc   3.1.3 @ /usr/bin/ (via rmarkdown)
 quarto   1.8.27 @ /usr/local/bin/quarto

─ Packages ───────────────────────────────────────────────────────────────────
 package    * version date (UTC) lib source
 broom      * 1.0.11  2025-12-04 [1] RSPM
 data.table * 1.18.0  2025-12-24 [1] RSPM
 ggdist     * 3.3.3   2025-04-23 [1] RSPM
 ggplot2    * 4.0.1   2025-11-14 [1] RSPM
 jsonlite   * 2.0.0   2025-03-27 [1] RSPM
 modelr     * 0.1.11  2023-03-22 [1] RSPM
 tidyr      * 1.3.2   2025-12-19 [1] RSPM

 [1] /home/runner/work/_temp/Library
 [2] /opt/R/4.5.2/lib/R/site-library
 [3] /opt/R/4.5.2/lib/R/library
 * ── Packages attached to the search path.

──────────────────────────────────────────────────────────────────────────────

Data Preparation

The loaded data are five conditions and their corresponding values.

# Load data
data <- data.table::fread(jsonlite::read_json("https://hiplot.cn/ui/basic/ggdist/data.json")$exampleData$textarea[[1]])
data <- as.data.frame(data)

# Convert data structure
data[, 1] <- factor(data[, 1], levels = rev(unique(data[, 1])))
data <- tibble(data)
data2 = lm(response ~ condition, data = data)
data3 <- data_grid(data, condition) %>%
  augment(data2, newdata = ., se_fit = TRUE)

# View data
head(data)
# A tibble: 6 Γ— 2
  condition response
  <fct>        <dbl>
1 A           -0.420
2 B            1.69 
3 C            1.37 
4 D            1.04 
5 E           -0.144
6 A           -0.301

Visualization

# Dist Plot
p <- ggplot(data3, aes_(y = as.name(colnames(data[1])))) +
  stat_dist_halfeye(aes(dist = "student_t", arg1 = df.residual(data2),
                        arg2 = .fitted, arg3 = .se.fit),
                    scale = .5) +
  geom_point(aes_(x = as.name(colnames(data[2]))),
             data = data, pch = "|", size = 2,
             position = position_nudge(y = -.15)) +
  ggtitle("ggdist Plot") + 
  xlab("response") + ylab("condition") +
  theme_ggdist() +
  theme(text = element_text(family = "Arial"),
        plot.title = element_text(size = 12,hjust = 0.5),
        axis.title = element_text(size = 12),
        axis.text = element_text(size = 10),
        axis.text.x = element_text(angle = 0, hjust = 0.5,vjust = 1),
        legend.position = "right",
        legend.direction = "vertical",
        legend.title = element_text(size = 10),
        legend.text = element_text(size = 10))

p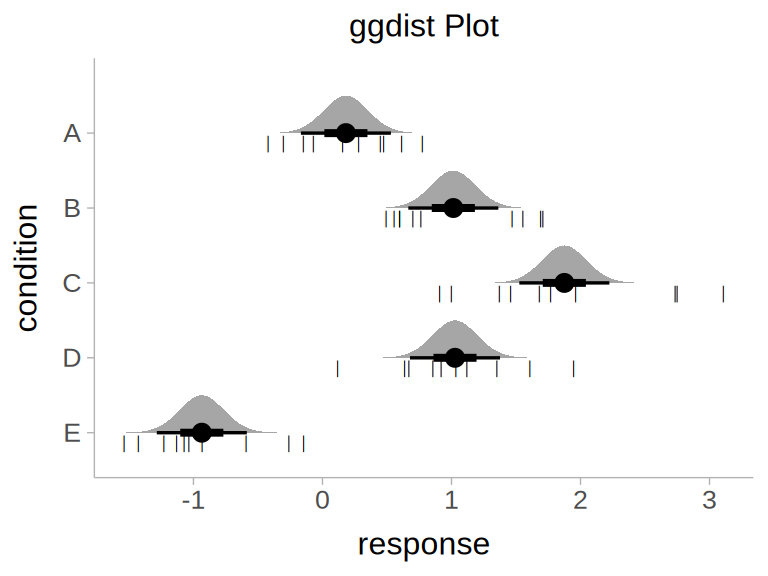
FigureΒ 1: Dist Plot

The diagram shows the confidence distribution of the mean under the conditions, and the approximate distribution of the corresponding values under the five conditions can be seen.