Line Regression

Note

Hiplot website

This page is the tutorial for source code version of the Hiplot Line Regression plugin. You can also use the Hiplot website to achieve no code ploting. For more information please see the following link:

https://hiplot.cn/basic/line-regression?lang=en

Linear regression is a regression method for linear modeling of the relationship between independent variables and dependent variables.If there is only one independent variable, it is called simple regression, and if there is more than one independent variable, it is called multiple regression.

Setup

• System Requirements: Cross-platform (Linux/MacOS/Windows)

• Programming language: R

• Dependent packages: data.table; jsonlite; ggrepel; ggplot2

# Install packages
if (!requireNamespace("data.table", quietly = TRUE)) {
  install.packages("data.table")
}
if (!requireNamespace("jsonlite", quietly = TRUE)) {
  install.packages("jsonlite")
}
if (!requireNamespace("ggrepel", quietly = TRUE)) {
  install.packages("ggrepel")
}
if (!requireNamespace("ggplot2", quietly = TRUE)) {
  install.packages("ggplot2")
}

# Load packages
library(data.table)
library(jsonlite)
library(ggrepel)
library(ggplot2)

sessioninfo::session_info("attached")

─ Session info ───────────────────────────────────────────────────────────────
 setting  value
 version  R version 4.5.2 (2025-10-31)
 os       Ubuntu 24.04.3 LTS
 system   x86_64, linux-gnu
 ui       X11
 language (EN)
 collate  C.UTF-8
 ctype    C.UTF-8
 tz       UTC
 date     2026-01-17
 pandoc   3.1.3 @ /usr/bin/ (via rmarkdown)
 quarto   1.8.27 @ /usr/local/bin/quarto

─ Packages ───────────────────────────────────────────────────────────────────
 package    * version date (UTC) lib source
 data.table * 1.18.0  2025-12-24 [1] RSPM
 ggplot2    * 4.0.1   2025-11-14 [1] RSPM
 ggrepel    * 0.9.6   2024-09-07 [1] RSPM
 jsonlite   * 2.0.0   2025-03-27 [1] RSPM

 [1] /home/runner/work/_temp/Library
 [2] /opt/R/4.5.2/lib/R/site-library
 [3] /opt/R/4.5.2/lib/R/library
 * ── Packages attached to the search path.

──────────────────────────────────────────────────────────────────────────────

Data Preparation

The loaded data are independent variables, dependent variables and groups.

# Load data
data <- data.table::fread(jsonlite::read_json("https://hiplot.cn/ui/basic/line-regression/data.json")$exampleData$textarea[[1]])
data <- as.data.frame(data)

# Convert data structure
data$group <- factor(data$group, levels = unique(data$group))

# View data
head(data)

  value1 value2 group
1   36.8  29.44    G1
2   54.0  43.20    G1
3   26.0  26.00    G1
4   39.0  31.20    G1
5   33.0  29.70    G1
6   29.0  34.80    G1

Visualization

# Line Regression
## Defining the equation
equation <- function(x, add_p = FALSE) {
  xs <- summary(x)
  lm_coef <- list(
    a = as.numeric(round(coef(x)[1], digits = 2)),
    b = as.numeric(round(coef(x)[2], digits = 2)),
    r2 = round(xs$r.squared, digits = 2),
    pval = xs$coef[2, 4] 
  )
  if (add_p) {
    lm_eq <- substitute(italic(y) == a + b %.% italic(x) * "," ~ ~
  italic(R)^2 ~ "=" ~ r2 * "," ~ ~ italic(p) ~ "=" ~ pval, lm_coef)
  } else {
    lm_eq <- substitute(italic(y) == a + b %.% italic(x) * "," ~ ~
  italic(R)^2 ~ "=" ~ r2, lm_coef)
  }
  as.expression(lm_eq)
}
## Plot
p <- ggplot(data, aes(x = value1, y = value2, colour = group)) +
  geom_point(show.legend = TRUE) +
  geom_smooth(method = "lm", se = T, show.legend = F) +
  geom_rug(sides = "bl", size = 1, show.legend = F) +
  scale_color_manual(values = c("#00468BFF","#ED0000FF")) +
  ggtitle("Line Reguression Plot") +
  theme_bw() +
  theme(text = element_text(family = "Arial"),
        plot.title = element_text(size = 12, hjust = 0.5),
        axis.title = element_text(size = 12),
        axis.text = element_text(size = 10),
        axis.text.x = element_text(angle = 0, hjust = 0.5,vjust = 1),
        legend.position = "right",
        legend.direction = "vertical",
        legend.title = element_text(size = 10),
        legend.text = element_text(size = 10))
  
## Add annotations for each group using ggrepel
repels <- rep("", nrow(data))
for (g in unique(data$group)) {
  fit <- lm(value2 ~ value1, data = data[data$group == g, ])
  v <- max(data[data$group == g, "value2"])
  repels[which(data$value2 == v)[1]] <- equation(fit, add_p = F)
}
p <- p + geom_text_repel(
  data = data,
  label = repels,
  size = 4,
  force = 5,
  label.padding = 5,
  na.rm = TRUE,
  min.segment.length = 100,
  show.legend = FALSE,
  nudge_x = 0,
  nudge_y = 0
  )

p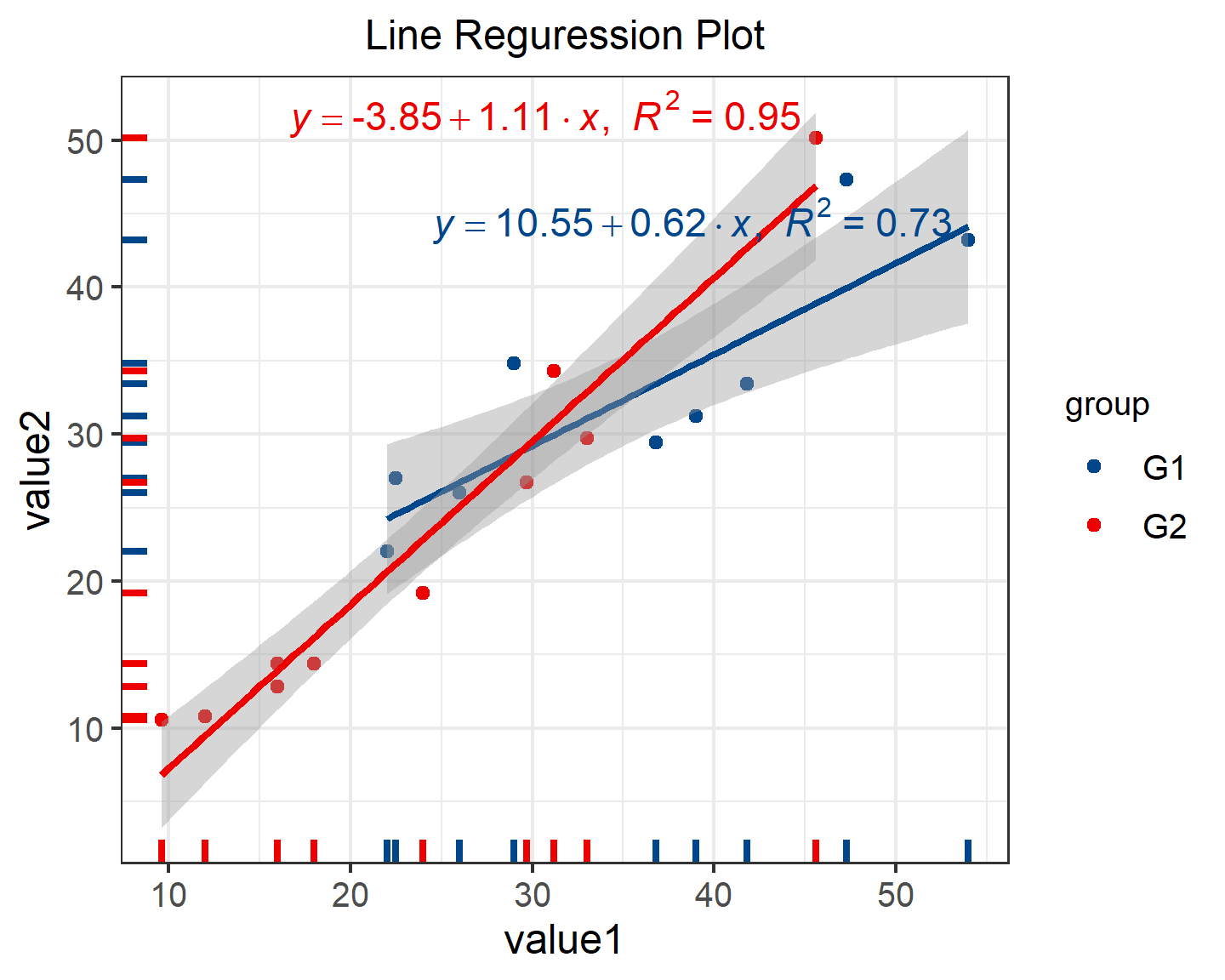

Figure 1: Line Regression

Different colors represent different groups, and linear regression equations can be added. The closer R squared is to 1, the closer the fitted curve is to the actual curve.