第 13 章工具

13.1 生成拉丁方

13.1.1 问题

你想要生成平衡序列用于实验。

13.1.2 方案

函数 latinsquare() (在下方定义) 可以被用来生成拉丁方。

latinsquare(4)
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    2    4    3
#> [2,]    2    1    3    4
#> [3,]    3    4    1    2
#> [4,]    4    3    2    1


# 生成两个大小为 4 的拉丁方(按顺序排列)
latinsquare(4, reps=2)
#>      [,1] [,2] [,3] [,4]
#> [1,]    3    4    1    2
#> [2,]    4    3    2    1
#> [3,]    1    2    4    3
#> [4,]    2    1    3    4
#> [5,]    4    2    1    3
#> [6,]    2    3    4    1
#> [7,]    1    4    3    2
#> [8,]    3    1    2    4


# 在调用该函数时最好加入一个随机种子 (random seed)，这样可以使得生成的拉丁方具有可重复性。
# 如下所示，这样做每次都会得到同一序列的拉丁方。
latinsquare(4, reps=2, seed=5873)
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    4    2    3
#> [2,]    4    1    3    2
#> [3,]    2    3    4    1
#> [4,]    3    2    1    4
#> [5,]    3    2    4    1
#> [6,]    1    4    2    3
#> [7,]    4    3    1    2
#> [8,]    2    1    3    4

存在大小为 4 的拉丁方 576 个。函数 latinsquare 会随机选择其中 n 个并以序列形式返回它们。这被称为重复拉丁方设计 。

一旦你生成了自己的拉丁方，你需要进行检查确保不存在许多重复的序列，因为这中情况在小型拉丁方中非常普遍 (3x3 or 4x4)。

13.1.2.1 生成拉丁方的函数

这个函数一定程度上使用了暴力算法来生成每个拉丁方，有时候它会因为没有可用的数字放入给定的位置而失败。这种情况下，它会再做尝试。可能存在一种更好的办法吧，但我并不清楚。

## - len 指定的是拉丁方的大小 - reps
## 是拉丁方的重复数-即给出多少个拉丁方 - seed
## 给定一个随机种子，这样可以保证生成的拉丁方是可重复的。
## - returnstrings
## 告诉函数为每个拉丁方返回一个字符串向量而不是返回一个巨大的矩阵，这个参数可以用来检查生成拉丁方的随机性。
latinsquare <- function(len, reps = 1, seed = NA, returnstrings = FALSE) {

  # 保存旧的随机种子并使用新的（如果有）
  if (!is.na(seed)) {
    if (exists(".Random.seed")) {
      saved.seed <- .Random.seed
    } else {
      saved.seed <- NA
    }
    set.seed(seed)
  }

  # 这个矩阵包含了全部独立的拉丁方
  allsq <- matrix(nrow = reps * len, ncol = len)

  # 如果需要，为每个拉丁方阵储存一个字符串 id
  if (returnstrings) {
    squareid <- vector(mode = "character", length = reps)
  }

  # 从向量中获取一个随机元素。(如果 x
  # 里只有一个元素，那么内置的示例函数会很诡异地发生不一样的运行）
  sample1 <- function(x) {
    if (length(x) == 1) {
      return(x)
    } else {
      return(sample(x, 1))
    }
  }

  # 生成 n 个独立的拉丁方阵
  for (n in 1:reps) {

    # 生成一个空的方阵
    sq <- matrix(nrow = len, ncol = len)

    # 如果我们从左上角开始依次填满这个方阵，那么某些拉丁方阵出现的概率就会比其他的大
    # 因此我们需要在方阵中随机地序列填充
    # 步骤大概如下： - 随机选择一个 NA 的单元格
    # (可以称之为目标单元格) -
    # 找出与目标单元格同行或同列的所有 NA 单元格 -
    # 填充目标单元格 - 填充同行/同列的其他单元格 -
    # 如果因为所有的数字都已被使用而无法继续填充单元格，那么就退出并重新开始填充一个新的方阵。
    # 简言之就是选择一个空单元格，填充它。然后以随机顺序填充与其“交叉”的其他空单元格。
    # 如果只是完全地随机填充（而没有沿着交叉方向），那么失败的概率非常高。

    while (any(is.na(sq))) {

      # 随机选择一个当前值为 NA 的单元格
      k <- sample1(which(is.na(sq)))

      i <- (k - 1)%%len + 1  # 获取行号
      j <- floor((k - 1)/len) + 1  # 获取列号

      # 在以 i,j 为中心的“交叉点”中找到其他为 NA
      # 的单元格
      sqrow <- sq[i, ]
      sqcol <- sq[, j]

      # 一个包含了所有 NA 单元格坐标的矩阵
      openCell <- rbind(cbind(which(is.na(sqcol)),
        j), cbind(i, which(is.na(sqrow))))
      # 随机化填充顺序
      openCell <- openCell[sample(nrow(openCell)),
        ]

      # 将中心单元格放到列表的最上面，这样保证从它开始填充方阵
      openCell <- rbind(c(i, j), openCell)
      # There will now be three entries for the center
      # cell, so remove duplicated entries
      # 要确保它是一个矩阵--否则，如果只是一行数据，它将会返回成一个向量并引起错误。
      openCell <- matrix(openCell[!duplicated(openCell),
        ], ncol = 2)

      # 填充中心位置，然后填充交叉方向上的其他空格
      for (c in 1:nrow(openCell)) {
        # The current cell to fill
        ci <- openCell[c, 1]
        cj <- openCell[c, 2]
        # 获取以 i,j
        # 为中心的“交叉”方向上中未使用的数字
        freeNum <- which(!(1:len %in% c(sq[ci, ],
          sq[, cj])))

        # 填充这些位置
        if (length(freeNum) > 0) {
          sq[ci, cj] <- sample1(freeNum)
        } else {
          # 错误的尝试 - 没有可获取的数值
          # 重新生成空方阵
          sq <- matrix(nrow = len, ncol = len)

          # 跳出循环
          break
        }
      }
    }

    # 将这单个拉丁方储存到包含所有拉丁方的矩阵中
    allsqrows <- ((n - 1) * len) + 1:len
    allsq[allsqrows, ] <- sq

    # 如果有需要，储存一个代表这个拉丁方的字符串。
    # 每个拉丁方都有一个唯一的字符串代号
    if (returnstrings) {
      squareid[n] <- paste(sq, collapse = "")
    }

  }

  # 恢复旧的随机种子（如果有）
  if (!is.na(seed) && !is.na(saved.seed)) {
    .Random.seed <- saved.seed
  }

  if (returnstrings) {
    return(squareid)
  } else {
    return(allsq)
  }
}

13.1.2.2 检查函数的随机性

一些生成拉丁方的算法并不是非常的随机。4x4 的拉丁方有 576 种，它们每一种都应该有相等的概率被生成，但有一些算法没法做到这一点。我们也许没有必要去检查上面函的随机性数，但如果要做这里确实可以通过一些代码来实现。我们运行下面的代码可以发现前面使用的算法其随机分布并不是很好。

这个代码创建 10,000 个 4x4 的拉丁方，然后计算这 576 个唯一拉丁方出现的频数。计数结果应该形成一个不是特别宽的正态分布；否则这个分布就不是很随机了。我相信期望的标准差是根号（10000/576）（假设随机生成拉丁方）。

# 设置要生成拉丁方的大小和数量
squaresize <- 4
numsquares <- 10000

# 获取指定大小的拉丁方的数量 (唯一方阵)
# 没有寻找到唯一的 nxn 方阵的通用解法
# 因此我们这里直接硬编码值 (来自
# http://oeis.org/A002860)
uniquesquares <- c(1, 2, 12, 576, 161280, 812851200)[squaresize]

# 生成拉丁方
s <- latinsquare(squaresize, numsquares, seed = 122, returnstrings = TRUE)

# 获取所有拉丁方阵的列表，并且进行计数
slist <- rle(sort(s))
scounts <- slist[[1]]

hist(scounts, breaks = (min(scounts):(max(scounts) + 1) -
  0.5))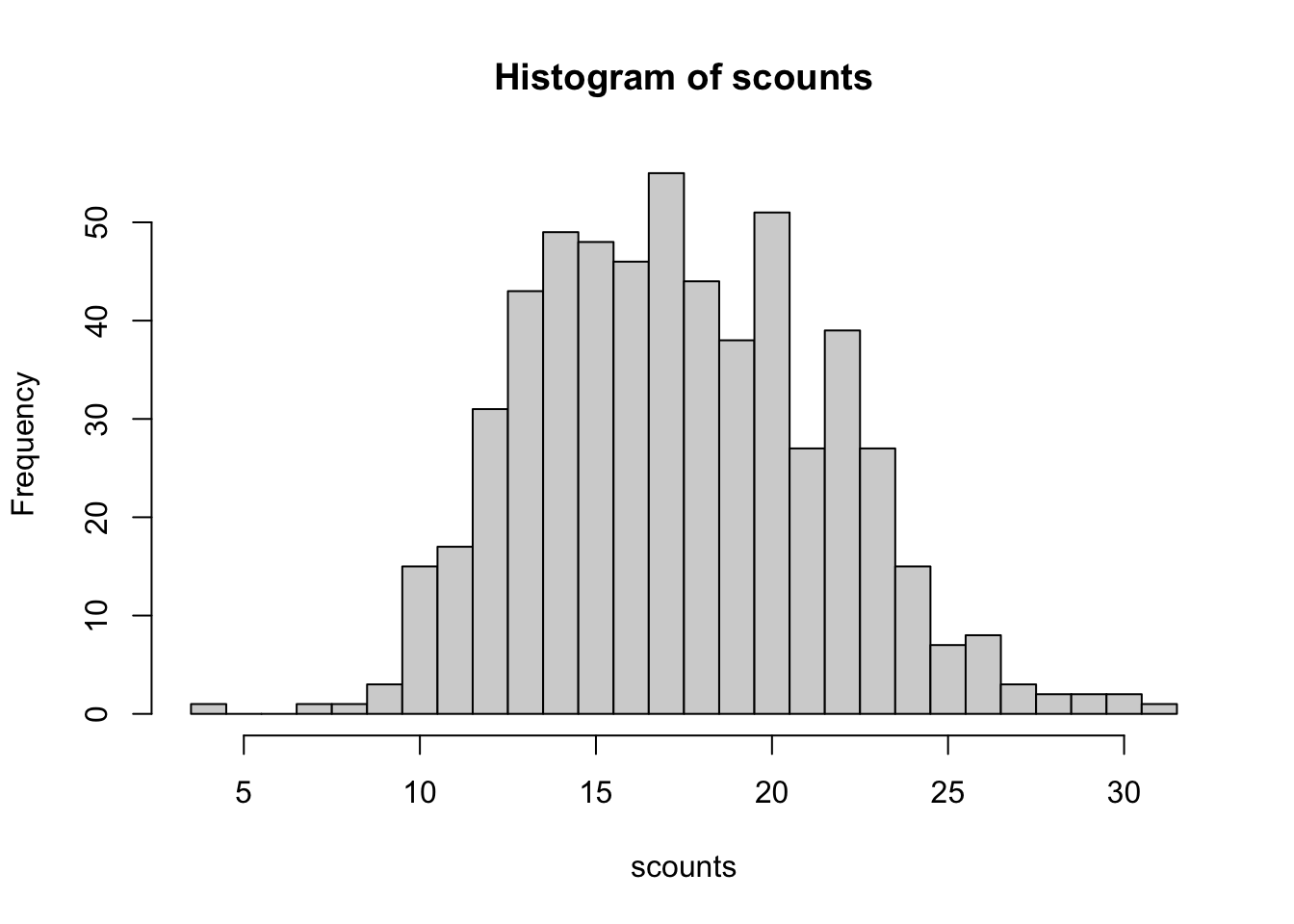

cat(sprintf("Expected and actual standard deviation: %.4f, %.4f\n",
  sqrt(numsquares/uniquesquares), sd(scounts)))
#> Expected and actual standard deviation: 4.1667, 4.2087

第 13 章 工具